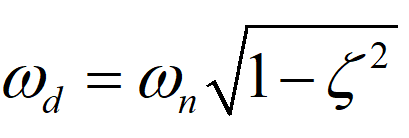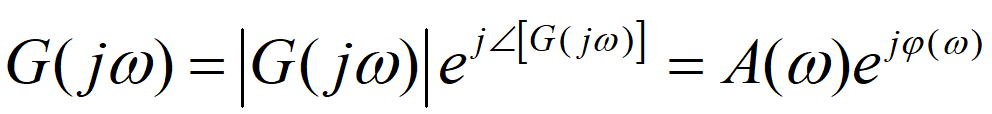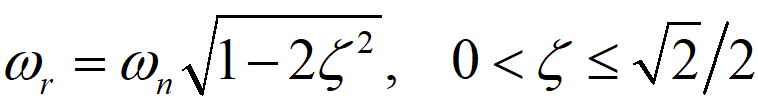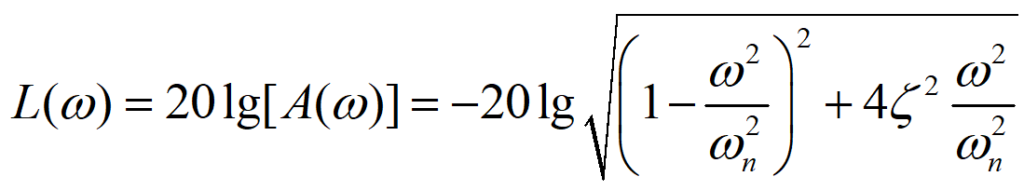自动控制原理学习笔记（一）

　　由于成电在微电子方向的本科课程中没有开设过自动控制原理相关课程，而信号与系统课程的要求也较低，在学习模拟集成电路中与频率响应相关的知识时总是感觉很难理解。因此最近（实际上是三个月前）自学了胡寿松的《自动控制原理》第七版，针对最初学习模拟集成电路时比较困惑的点在此做一些总结。

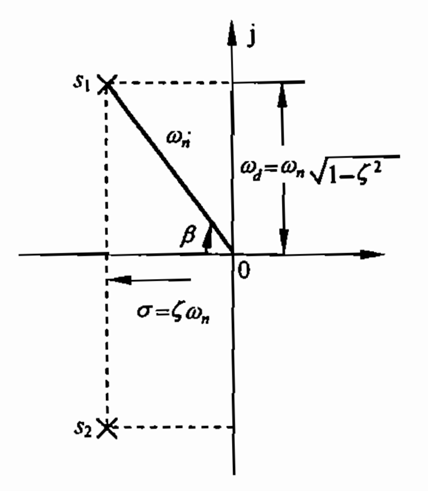
　　当时困扰我的第一个问题是，在频率分析时出现的共轭极点/零点，在画波特图时以及在平时分析的极点频率时，究竟是以该极点在s平面上的幅值、实轴频率还是虚轴频率为准呢？以下以自动控制原理以及模拟电路中常见的二阶系统（一对左半平面共轭极点）为例，分析其s平面坐标对应的物理意义。

二阶系统频域分析

　　一个二阶系统传递函数的标准形式为：

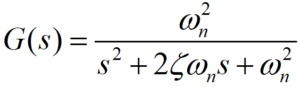
　　其中，ω_n为自然频率（sansen的模集中称为谐振频率），ζ为阻尼比，当0<ζ<1时，其对应的s域上的共轭复极点对如图1所示。

　　如图1所示，s₁、s₂为一对左半平面复极点对，其幅值为自然频率ω_n，与实轴的负半轴夹角为阻尼角 β，阻尼比ζ = cos β。该极点的实部为衰减系数 σ = ζβ，虚部为阻尼震荡频率

　　通过拉普拉斯逆变换，可以计算出欠阻尼二阶系统的单位阶跃响应为：

　　即阻尼振荡频率ω_d为共轭极点组成的欠阻尼二阶系统的减幅震荡频率，随着阻尼比ζ从0变化到1（即从无阻尼到临界阻尼），ω_d从ω_n变化到0，即从以自然频率震荡变为不震荡。

　　而当分析频域响应时，取G(s)中的s=jω，则其可以化为：

　　其中，A(ω) = |G( jω)|和φ(ω) = ∠[G( jω)]分别为系统在频率为ω的正弦信号作用下输出信号与输入信号的幅值比和相位差，也即波特图中的幅频曲线与相频曲线。

　　对于上述的二阶系统，代入s=jω，可以计算出：

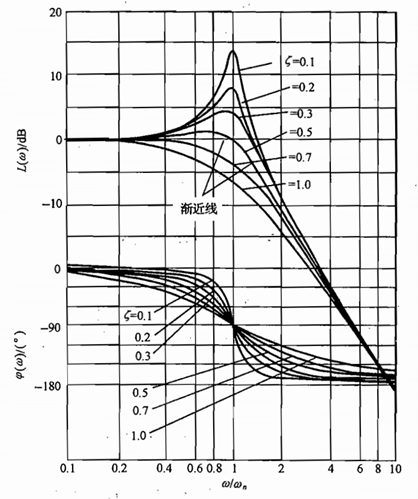
　　其中相位 φ(ω) 分段是为了保证相角连续的从第Ⅳ象限变化到第Ⅲ象限，该公式所对应的准确的幅频与相频特性图2所示。

　　其中，幅频曲线中的峰值称为谐振频率ω_r（与sansen中的谐振频率不同），可以通过对A(ω) 求导并使其等于0计算得到为：

　　在该频率的谐振峰值为：

　　可以看出，当阻尼比 ζ→0 时，ω_r →ω_n，A(ω_r) →∞。而当 ζ=√2/2时，ω_r= 0，A(ω_r) =1，不会出现任何尖峰。

　　而当绘制近似的波特图时，一般会忽略尖峰，考虑到其对数幅频特性为：

　　当ω<< ω_n时，L(ω) ≈ 0，低频近似为0dB的直线；而当ω >> ω_n时，L(ω) ≈ -40lg(ω/ω_n)，高频的渐进线为过(ω_n,0)点，斜率为-40dB/dec的直线，也即认为绘制波特图时的极点频率为ω_n。

　　总结一下，对于一个常见的二阶欠阻尼系统（ 0<ζ<1）：

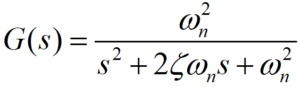
　　有三个关键频率，分别为：

　　1. 自然频率ω_n：为其s域上极点的幅值，也是绘制近似波特图时的极点频率。

　　2. 阻尼振荡频率：为其s域上极点的虚轴频率，也是时域单位阶跃响应的减负振荡频率。

　　3. 谐振频率：为其频域响应的幅频特性曲线的峰值。

　　第一次在博客写文章，很多地方，尤其是公式和字体等方面还有很大的问题，不过好歹赶在2022年的最后一天发出来了，之后再研究一下如何让公式和字体更加好，重新编辑一下这篇文章。